الإزاحة الزاوية مقسمومة على الزمن تسمى
متوسط السرعة الزاوية (بالانجليزية: The Average Angular Velocity)
تسمى الإزاحة الزاوية مقسمومة على الزمن بمتوسط السرعة الزاوية، وهو مفهوم فيزيائي مُتجه يُعبر عن التغير في الإزاحة الزاوية (θ =ثيتا) على طول دائرة بالنسبة للزمن، يُعبر عن متوسط السرعة الزاوية رمزيًا بالصيغة ![]() ووحدته ه
ووحدته ه![]() أو راديان/ الثانية.
أو راديان/ الثانية.
والسرعة الزاوية مثلها مثل الإزاحة الزاوية كمية مُتجهة تعتمد على اتجاه دوران الجسم على مُحيط الدائرة، ويُمكن تحديد اتجاه الدوران بواسطة استخدام قاعدة اليد اليُمنى حيث تُشير القيمة:
- الموجبة إلى دوران الجسم عكس عقارب الساعة.
- السالبة إلى دوران الجسم مع عقارب الساعة.
يتم حساب متوسط السرعة الزاوية من خلال التطبيق المُباشر للمعادلات التالية:
متوسط السرعة الزاوية = التغير في الإزاحة الزاوية (ΔΘ) ÷ التغير في الزمن (Δt)
∴ متوسط السرعة الزاوية = ⌈الإزاحة الزاوية النهائية Θ2 – الإزاحة الزاوية الإبتدائية Θ1⌉ ÷ ⌈ الزمن النهائي t2 – الزمن الإبتدائي t1⌉
وبالتالي يُمكن صياغته فيزيائيًا على النحو التالي :
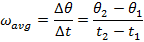
حيث يُشير كل رمزٍ من الرموز الموضحة إلى قيمة فيزيائية مُحددة:
- أولًا،
![الإزاحة الزاوية مقسمومة على الزمن]() = متوسط السرعة الزاوية (بالإنجليزية: average angular velocity) ووحدته
= متوسط السرعة الزاوية (بالإنجليزية: average angular velocity) ووحدته  = راديان / الثانية.
= راديان / الثانية. - ثانيًا،
![]() = التغير في الإزاحة الزاوية الحادثة ووحدته الراديان (بالانجليزية: Radian) ورمزه rad أو c.
= التغير في الإزاحة الزاوية الحادثة ووحدته الراديان (بالانجليزية: Radian) ورمزه rad أو c. - ثالثًا،
 = التغير في الزمن على طول الحركة ويُقاس بالثانية.
= التغير في الزمن على طول الحركة ويُقاس بالثانية. - رابعًا،
![]() = الإزاحة الزاوية الإبتدائية ووحدته الراديان.
= الإزاحة الزاوية الإبتدائية ووحدته الراديان. - خامسًا،
![]() = الإزاحة الزاوية النهائية ووحدته الراديان.
= الإزاحة الزاوية النهائية ووحدته الراديان. - سادسًا، t1 = الزمن الإبتدائي ويُقاس بالثانية.
- سابعًا، t2 = الزمن النهائي يُقاس بالثانية. [1]
وللفهم الجيد للسرعة الزاوية يجب الوقف على عدد من المُصطلحات الفيزيائية ومُحاولة توضيحها مثل:
- مفهوم الراديان.
- مفهوم الإزاحة الزاوية.
ما هو الراديان
الراديان وحدة دولية مشتقة لقياس الزوايا وهو نظام قياسي بديلًا لقياس الزوايا بنظام الدرجات على محيط الدائرة
والراديان (بالانجليزية: Radian) مُصطلح رياضي فيزيائي يُعبر عن الزاوية المُتشكلة نتيجة دوران نقطة على محيط الدائرة بمقدار نصف القطر ويتم التعبير عنه رياضيًا برمزي rad أو c.
ويُعتبر الراديان وحدة دولية مشتقة لقياس الزوايا ونظام قياسي بديلًا لقياس الزوايا بنظام الدرجات على محيط الدائرة ويُستخدم عادة في المعادلات الرياضية والفيزيائية المُتقدمة على النحو التالي: [2]
الراديان الواحد = 180 درجة ⁄ π أي مايُساوي 57.295 درجة
ومنه يُمكننا القول أن:
زاوية مقدارها 360 درجة = 2π راديان
زاوية مقدارها 180 درجة = π راديان
ولفهم الطريقة الاستنتاجية المنطقية المُتبعة للوصول إلى قيمة الراديان الواحد يُمكنك الإستماع إلى الفيديو التوضيحي التالي
ما هي الإزاحة الزاوية
التغير في زاوية الدوران أثناء حركة الجسم
الإزاحة الزاوية (بالانجليزية:rotational motion) مفهوم فيزيائي يُعبر عن التغير في الزاوية أثناء دوران الجسم ويُعبر عنها رمزيًا بـ (ΔΘ = دلتا ثيتا) وتُقاس بوحدة الرديان (rad).
والإزاحة الزاوية كمية مُتجهة تعتمد على اتجاه دوران الجسم على مُحيط الدائرة، ويُمكن تحديد اتجاه الدوران بواسطة استخدام قاعدة اليد اليُمنى حيث تُشير القيمة:
- الموجبة إلى دوران الجسم عكس عقارب الساعة.
- السالبة إلى دوران الجسم مع عقارب الساعة.
وتُستخدم الإزاحة الزاوية لإيجاد:
- المسافة التي تتحركها نقطة واقعة على جسم دوار (d) بالمتر.
- السرعة الزاوية.
أولًا، إيجاد المسافة التي تتحركها نقطة واقعة على جسم دوار (d): لإيجاد المسافة التي تقطعها نقطة على جسم يدور بشكل مستمر يجب إيجاد:
- ثيتا (Θ) أو زاوية الدوران بوحدة الراديان.
- نصف قطر الدائرة (r) بالمتر.
وبالتطبيق المُباشر على المعادة التالية d = Θ X r يُمكننا إيجاد المسافة المقطوعة بشكلٍ دقيق.
وللتدرب على المسائل والتمارين الموضوعة دراسيًا للربط بين المسافة المقطوعة والإزاحة الزاوية يُمكنك الإستماع الى الفيديو التعليمي القادم ومُحاولة التدرب على الأنواع المُختلفة من الأسئلة. [3]
مسائل تطبيقية على متوسط السرعة الزاوية
السؤال الأول: يتحرك بندول الساعة الكبير بين زاويتين هما 17π/12 راديان و 19π/12 راديان خلال ثانية واحدة، ماهو متوسط السرعة الزاوية للبندول أثناء تحركه
المُعطيات :
- أولًا،
 = الإزاحة الزاوية الإبتدائية = 17π/12 راديان
= الإزاحة الزاوية الإبتدائية = 17π/12 راديان - ثانيًا،
![]() = الإزاحة الزاوية النهائية = 19π/12 راديان
= الإزاحة الزاوية النهائية = 19π/12 راديان - ثالثًا،
 = التغير في الزمن على طول الحركة = ثانية واحدة.
= التغير في الزمن على طول الحركة = ثانية واحدة.
الحل:
بالتطبيق المُباشر على القانون الحسابي الخاص بــ :
- التغير في الإزاحة الزاوية (ΔΘ)
- متوسط السرعة الزاوية
![]() .
.
أولًا، حساب التغير في الإزاحة : يُمكن حساب التغير في الإزاحة الزاوية مباشرة عن طريق تطبيق المعادلة التالية
التغير في الإزاحة الزاوية (ΔΘ) = الإزاحة الزاوية النهائيةΘ2 – الإزاحة الزاوية الإبتدائيةΘ1
∴ التغير في الإزاحة الزاوية (ΔΘ)= (19π/12 راديان) – 17π/12 راديان = π/6 راديان .
ثانيًا، حساب متوسط السرعة الزاوية : يُمكن حساب متوسط السرعة الزاوية مباشرة عن طريق تطبيق المعادلة التالية:
متوسط السرعة الزاوية = التغير في الإزاحة الزاوية (ΔΘ) ÷ التغير في الزمن (Δt)
∴ متوسط السرعة الزاوية =π/6 راديان ÷ 1 ثانية = π/6 راديان / الثانية
السؤال الثاني: تدور مروحة مُعلقة في السقف بمقدارة من السرعة الزواية متوسطها 7000 راديان / الثانية، كم عدد الثواني التي تحتاجها المروحة لتدور بزاوية مقدارها 180 درجة
المُعطيات :
![]() = متوسط السرعة الزاوية = 7000 راديان / الثانية
= متوسط السرعة الزاوية = 7000 راديان / الثانية
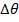 = التغير في الإزاحة الزاوية الحادثة = 180 درجة = π راديان
= التغير في الإزاحة الزاوية الحادثة = 180 درجة = π راديان
الحل:
بالتطبيق المُباشر على القانون الحسابي الخاص بــ متوسط السرعة الزاوية = التغير في الإزاحة الزاوية (ΔΘ) ÷ التغير في الزمن (Δt).
وبالتالي فإن التغير في الزمن (Δt) = التغير في الإزاحة الزاوية (ΔΘ) ÷ متوسط السرعة الزاوية ![]()
∴ (Δt) = π راديان ÷ 7000 راديان / الثانية = 0.000449 ثانية. [1]
المحتويات المرئية المُتاحة إلكترونيًا لدراسة الإزاحة الزاوية مقسمومة على الزمن
- الفيديوهات التعليمية المُقدمة على منصة مدرسة ضمن مبادرة محمد بن راشد ال مكتوم العالمية لاثراء المحتوى التعليمي العربي، وللإطلاع على المزيد من سلسلة الفيزياء التعليمية يُرجى الضغط على هذا الرابط.
- الفيديو التعليمي المُقدم ضمن سلسلة دروس الفزياء للصفوف الثانوية والمُقدمن من أحد أساتذة الفزياء.


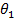 = الإزاحة الزاوية الإبتدائية ووحدته الراديان.
= الإزاحة الزاوية الإبتدائية ووحدته الراديان.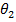 = الإزاحة الزاوية النهائية ووحدته الراديان.
= الإزاحة الزاوية النهائية ووحدته الراديان.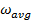 .
.
التعليقات مغلقة.