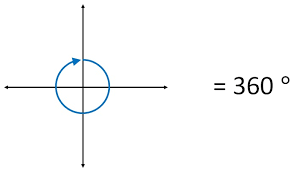
كيف تقاس الزوايا
تُقاس الزاوية بوحدة تسمى
الدرجة .
تقاس الزاوية بوحدة تسمى الدرجة. حيث يتم تقسيم الدائرة إلى 360 درجة. والزاوية القائمة تساوي 90 درجة، وهي تساوي ¼ من الزاوية 360 درجة. من الزوايا الشهيرة الأخرى التي نراها بكثرة في الأشكال الهندسية، الزاوية 180 درجة وهي ½ من 360 درجة. والزاوية 45 درجة وهي ½ من الزاوية 90 درجة.
يمكن قياس الزاوية بواحدة أخرى هي الراديان. ويعتبر كل من الراديان والدرجة واحدات قياس للزاوية. والراديان تحدد طول قوس الدائرة على نصف قطر تلك الدائرة.
من الأمور الشائعة والتي يجب علينا معرفتها فيما يخص الزاويا الشهيرة بالراديان هي:
- 180 درجة = باي راديان (باي هو ثابت الدائرة الشهير 𝜋)
- 360 درجة = 2 باي راديان
- 90 درجة = ½ باي راديان
ويتم قياس الزوايا بثلاثة أنظمة: وهي النظام المئوي لقياس الزوايا، النظام الدائري لقياس الزوايا، النظام الستيني لقياس الزوايا.
تعريف الزاوية
الزاوية هي الأرقام الناتجة من اتحاد خطين واشتراكهما في نقطة واحدة هذه النقطة تسمى رأس الزاوية والضلعان الآخران هما ضلعي الزاوية لذلك فلابد أن يتقاطعا الخطان في نقطة أما الخطان المتوازيان فلا يكونان زاوية فإذا كان أحد الضلعين عمودي على الآخر تنتج زاوية قائمة قياسها 90درجة ، أما إذا كان الخطان يلتقيان في نقطة ولكن الضلعين يقتربان من بعضهما يصنعان زاوية حادة يكون قياسها أقل من 90 ، أما إذا كان الخطان متباعدان فيصنعان زاوية منفرجة قياسها أكبر من 90 وأقل من 180 درجة ، كما يوجد الزاوية المستقيمة وهي مسطحة قياسها 180 درجة ، أما الزاوية الدائرية فهي يكون قياسها مساويا ل 360 درجة وهذه هي
أنواع الزوايا وقياساتها
من حيث القياس .
كيف تقاس الزوايا!! يتم قياس الزوايا من خلال العديد من عناصر القياس ، والتحليل مثل المنقلة وقد يتم قياسها بدون منقلة من خلال حساب المثلثات من خلال قياس طول قوس الدائرة والذي يسمى باي ولإيجاد المحيط من خلال مربع طول القوس المحصور بين ضلعي الزاوية ومحيطها والزاوية في الأصل هي كلمة لاتينية وقد عرفها العالم إقليدس الميل أحد المستقيمين على الآخر وتقاس الزاوية بوحدة الدرجة وهي قياس الزاوية مستوية ، تمثل 1/360 من دوران كامل عادة ما يتم الإشارة إليه بـ
°
أما أنواع الزوايا من حيث اتجاهاتها فتكون الزوايا المعطاة بعلامة هي زوايا موجبة إذا تم قياسها عكس اتجاه عقارب الساعة ، وزوايا سالبة إذا تم قياسها في اتجاه عقارب الساعة ، من خط معين إذا لم يتم تحديد خط ، فيمكن افتراض أنه المحور السيني في المستوى الديكارتي يوجد في كثير من الحالات ذات الطابع الهندسي .
كيفية قياس الزوايا المختلفة
لو تسائلنا كيف تقاس الزوايا!! أو ما هي الأداة المستعملة، فهي المنقلة. يتم قياس الزاوية من خلال أداة تسمى المنقلة ويتم عمل عدد من الخطوات وهي:
- يتم رسم خط مستقيم ويكون له بداية ونهاية ويمكنك استخدام الحافة المسطحة لمقياس الزوايا ويتم رسم هذا الخط من خلال المسطرة ويكون الخط بمقياس معين ثم ضع المؤشر على المنقلة في أي مكان على الخط الذي تم رسمه ولابد من الأخذ في الإعتبار أن يكون جانب الزاوية كبيرًا بدرجة كافية ليتجاوز المحيط الخارجي لمقياس الزوايا أما إذا كان جانب الزاوية لا يتجاوز قوس المنقلة فلابد من مد الخط المستقيم ليتلاقى الخطان مع جانب الزاوية
-
قم باستدارة المنقلة وتحريكها حتى يصبح الخط أعلى أحد أضلاع الزاوية ثم قم بتحريك المنقلة برفق للحفاظ على دقة القياس وليكون
خط قاعدة المنقلة فوق أحد ضلعي الزاوية بالضبط ومراعاة أن يكون خط القاعدة موازي لحافة المنقلة وليس الحافة ذاتها، وهو يمر بمركز المنقلة من نقطة الصفر في ناحية إلى نقطة الصفر المقابلة. - تذكر أن القاعدة موازية للحافة ، ولكنها ليست الحافة المسطحة للمنقلة ثم يتم محاذاته مع مركز الأصل ويمتد الخط على كلا الجانبين من نقطة البداية في المقياس التدريجي والنقطة التي تتوسط المنقلة تسمى المركز اجعل هذه النقطة فوق رأس الزاوية ليكون القياس دقيق وصحيح.
- وعندما يتقاطع ضلعي الزاوية عند نقطة بحيث يتوازى الضلعان للزاوية المراد قياسها وفي أي نقطة يتقاطع مع التدرج حينها فإن الرقم الذي سوف يمر بالخط من خلاله فيكون هو قياس الزاوية.
أنظمة قياس الزوايا
هناك ثلاثة أنظمة لقياس الزوايا وهم:
-
النظام المئوي لقياس الزوايا
وهو يتم فيه تقسيم الدائرة إلى 400 قسم ويندرج القسم الواحد إلى مسمى الدرجة المئوية ويرمز له بالرمز (g) وتقسم الدرجة الواحدة أيضا إلى مائة جزء يسمى الجزء الواحد منها بالدرجة المئوية ويرمز لها بالرمز c ثم تقسم الوحدة المئوية إلى مائة جزء يسمى الجزء الواحد بالثانية المئويةيُعتقد أن البابليين اخترعوا الدرجة ودائمًا ما يُحسبون في الأساس 60هذا هو المكان الذي ظهرت فيه الأفكار الأولية لـ 360
-
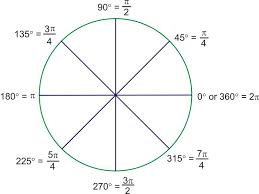
النظام الدائري لقياس الزوايا
ويتم القياس بوحدة تسمى الراديان ويرمز لها بالرمز(r) وتعرف بأنها تلك الزاوية المركزية التي تكون محصورة بين قوسين من الدائرة يكون طوله مطابق لطول نصف قطر الدائرة وهي تساوي النسبة بين طول القوس المقابل لها مع نصف قطر الدائرة وتقاس الزاوية المركزية من خلال طول القوس ÷ طول نصف القطر ويمكن أن يساعد قياس الزوايا في تحسين الفهم المكاني والعلاقة بين الأرقام والقياسات ، وهو ليس مفيدًا فقط في الأكاديميين ولكن التعرف على الزوايا يساعدنا على فهم واستخدام الأشياء من حولنا.
-
النظام الستيني لقياس الزوايا
وفيه تقسم الدائرة إلى 360 قسم يسمى القسم الواحد بالدرجة الستينية ويرمز له بالرمز (
°
) كما يتم تقسيم الجزء الواحد إلى 60 جزء لذلك تم تسميته بالنظام الستيني ويسمى الجزءالواحد بالدقيقة الستينية ثم تقسم كل وحدة إلى الثانية الستينية ويرمز لها بالرمز(“) لذلك فإنه يمكن استنتاج أن كل درجة ستينية= 60 دقيقة ستينية= 3600 ثانية ستينية.[1]

الزوايا المتكاملة والمتجاورة والمتتامة
الزوايا المتكاملة:
هي زوايا مجموعها 90 درجة ( أي زاوية قائمة واحدة) والأخرى تسمى مكملة للأخرى.
فمثلا عندما تكون قياس الزاويتان 60 درجة ، 30 درجة هما زاويتان متكاملتان لأن 60 درجة + 30 درجة = 90 درجة فإن الزاوية التكميلية التي قياسها 60 درجة هي قياس الزاوية 30 درجة كما أن
الزوايا وقياساتها
تتكامل مع بعضها لتكون المثلث والتي قياس كل زاوية منهيكون مجموعهم 180لذلك فإن الزاويتان اللتان مجموعهما دائرة كاملة واحدة (360 درجة) تسمى الزوايا التكميلية أو الزوايا المترافقة لأنهما يكملان بعضهما الآخر وتسمى الزاوية الأصغر عند النقطة التي يلتقي فيها خطان بالزاوية الداخلية وتضاف قياسات الزوايا الداخلية للمثلث ما يصل إلى
π
راديان ، أو 180 درجة كما تضيف قياسات الزوايا الداخلية لشكل رباعي بسيط ما يصل إلى 2
π
راديان
الزوايا المتجاورة:
يقال إن زاويتين غير متداخلتين هما زاويتان متجاورتان إذا كان لديهما رأس مشترك ، ذراع مشترك ، ذراعان آخران مستلقيان على الجانب المقابل من هذا الذراع المشترك ، بحيث لا تتداخل أجزاؤهما الداخلية كما أن الزوايا التي تشترك في رأس وحافة مشتركة ولكن لا تشترك في أي نقاط داخلية تسمى الزوايا المتجاورة .
الزوايا المتقابلة عموديًا:
تسمى الزاويتان المكونتان من خطين متقاطعين ليس لهما ذراع مشترك بزوايا متقابلة رأسيًا ويقال إن زاويتين متجاورتين تشكلان زوجًا خطيًا إذا كان مجموعهما 180 درجة.
الزوايا المتتامة
: عبارة عن زاوية تكون تامة للزاوية الأخرى من حيث القياس وهما متجاورين ويكون مجموعهما 90 درجة كما هو معروف أن للمثلث ثلاث زوايا ومجموع تلك الزوايا لابد أن يكون 180 درجة كما يوجد ما يسمى بالزوايا الخارجية ، والداخلية وهي أيضا متممة لبعضهما البعض كما أن في الزاوية المتتامة لابد أن يتحقق شرط التطابق بحيث يكون المستقيمين متوازيين والثالث متطابق لهما ويشكلان الزاويتان المتتامتان مقدار ربع دائرة كما تسمى الزاوية المكملة للمقدار 90 درجة بالزاوية التامة أما إذا كانتا الزاويتان متجاورتان فتكون الأضلاع مشتركة لتكوين زاوية قائمة كما يشمل المثلث القائم الزاوية زاويتان متتاليتان ويكونان حادتين لأن زوايا المثلث 180 وهناك زاوية قائمة فبالتالي تكون الزاويتين حادتين .[2]